Drei gängige optische Bildgebungssysteme

Auf der Grundlage der Untersuchung der verschiedenen Phänomene der Lichtübertragung wurden verschiedene optische Instrumente entwickelt und hergestellt, wie Mikroskope zur Beobachtung von kleinen Objekten, Teleskope zur Beobachtung von Objekten in der Ferne, Kameras, Kameras und so weiter.

In optischen Instrumenten gibt es in der Regel ein optisches System, dessen Aufgabe es ist, das beobachtete Objekt für die menschliche Augenbeobachtung abzubilden oder mit optoelektronischen Geräten zu erfassen.

Ein optisches System besteht normalerweise aus einem oder mehreren optischen Elementen. Jedes optische Element besteht aus einem Medium mit einem bestimmten Brechungsindex, das von einer kugelförmigen, planaren oder asphärischen Oberfläche umgeben ist.

Das optische System, in dem die Oberflächenkrümmung der einzelnen optischen Elemente, aus denen das optische System besteht, auf der gleichen Linie ist, wird als ein coaxiales optisches System bezeichnet, und diese Linie wird als optische Achse bezeichnet.

Es gibt auch Nicht-Koaxial-Optik-Systeme (z. B. Spektrometer-Systeme, die Streuung Prismen oder Streuung Gitter enthalten).

Alle optischen Elemente in einem optischen System bestehen aus einer Kugel, das sogenannte Kugel-System.

Wenn ein optisches System asphärische Oberflächen enthält, wird es als asphärisches System bezeichnet.

Eine einzelne Linse ist die grundlegende Einheit eines Koaxialkugelensystems.

Die Linse kann je nach Form in zwei Kategorien unterteilt werden: Die erste Klasse wird als konvergente Linse oder positive Linse bezeichnet, die durch eine mittlere Dicke und dünne Kante gekennzeichnet ist. Die zweite Art ist die diffuse Linse oder negative Linse, die durch die mittlere dünne, dick auf beiden Seiten gekennzeichnet ist.

Entsprechend dem Gesetz der Lichtverbreitung und der Wellenfront wird die Verbreitung des Strahls durch die Linse untersucht.

(1) konvergierende Linse oder positive Linse

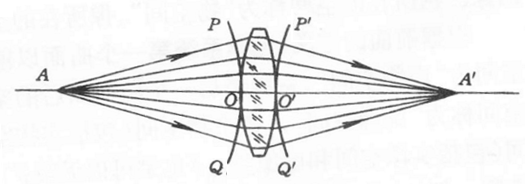
Wie in Abbildung 1 gezeigt, ist für den konzentrischen Strahl, der vom Punkt A emittiert wird, die Wellenfront PQ eine Kugel mit A als Mittelpunkt. Wenn der Strahl durch die Linse passiert, weil der Brechungsindex des Glases größer ist als der Brechungsindex der Luft, basierend auf der Beziehung zwischen der Brechungsrate und der Lichtgeschwindigkeit, die Lichtgeschwindigkeit im Glas ist kleiner als die Geschwindigkeit der Übertragung in der Luft, wird die Dicke des Zentrums der Linse größer als die Dicke der Kante, so dass der zentrale Teil langsamer ist, während der Rand Teil schneller ist. Im Falle von Abbildung 1 ist das Licht an der Kante bereits von P und Q zu P'', Q' und die Emissionswellenfläche ist von links nach rechts gebogen, und der gesamte Strahl ist in Richtung der Lichtachse gefaltet, was als "Gemeinschaft" bezeichnet wird. Wenn die Linsenoberfläche eine geeignete Oberflächenform wählt, kann die Emissionswellenoberfläche immer noch eine Kugel sein. Die entsprechenden Strahlen schneiden sich am Punkt A’, der offensichtlich das Zentrum der emittierten Oberflächenwelle ist. "A" ist ein "Wie-Punkt", der von Punkt A durch die Linse gebildet wird, und Punkt A wird als "Objektpunkt" bezeichnet.

In Abbildung 1 ist A 'der Schnittpunkt des tatsächlichen Lichts. Wenn Sie den Bildschirm auf "A" setzen, können Sie einen hellen Punkt auf dem Bildschirm sehen, der als "Realisierungspunkt" bezeichnet wird.

(2) Differentielle Linse oder negative Linse

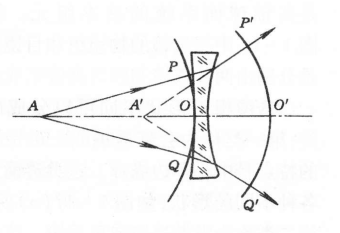
Da die Kanten der diffusen Linse dicker als die Mitte sind, breitet sich der zentrale Teil des Strahls schneller aus als die konvergente Linse, während die Kanten langsamer ausbreiten. wie in Bild 2 dargestellt. Nachdem der Strahl die Linse durchläuft, biegt sich die Wellenfläche nach links, und das entsprechende emittierte Licht wird nach außen abgelenkt, was als "Divergenz" bezeichnet wird. Wenn die Emissionswellenfläche eine Kugel ist, gehen alle Lichtverlängerungen durch den Kern A' der Kugelwelle. Wenn man von hinten die Kamera betrachtet, sieht man genau das gleiche Licht, das von A' emittiert wird, kann aber nicht auf dem Bildschirm angezeigt werden. Solche Punkte werden als „Imagine Punkte“ bezeichnet.

In Abbildung 1 und Abbildung 2 ist der Punkt A der Ausgangspunkt des tatsächlichen Lichts, der als "Objektpunkt" bezeichnet wird.

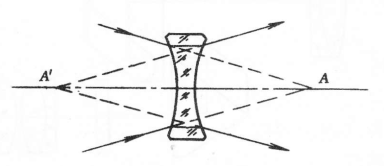
Wenn der Punkt A kein tatsächlicher Lichtpunkt ist, sondern ein Bildpunkt eines anderen optischen Systems, beginnt er, die Ausbreitungsrichtung zu ändern, bevor das Licht den Punkt A erreicht, bevor er die erste Seite des postoptischen Systems trifft, wie in Abbildung 3 dargestellt. Der tatsächliche Lichtstrahl passiert zu diesem Zeitpunkt nicht durch den Punkt A, sondern seine Verlängerungslinie schneidet sich an dem Punkt A, der als "Imagent Point" bezeichnet wird.

(3) Koaxiales optisches System

Stellen Sie O1, O2, L, Ok für ein optisches System mit k-Face dar, wie in Abbildung 4 dargestellt.

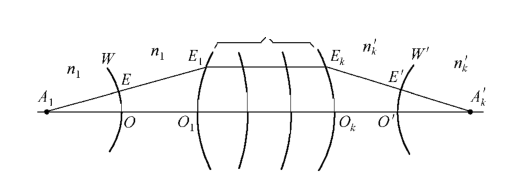
Die sphärische Welle wird vom leuchtenden Punkt A1 emittiert und der konzentrische Strahl am Punkt A1 emittiert, der Punkt A wird als Punkt bezeichnet. Wenn die Kugel eine Kugelwelle bleibt, nachdem sie das optische System durchlaufen hat, d. h. ein konzentrierter Strahl, der mit dem Punkt Ak 'mitten ist, und der Punkt Ak 'ist auch ein geometrischer Punkt, dann ist das perfekte Bild für A1. Daher ist die Bedingung für ein perfektes Bild von optischen Systemen, dass, wenn die eingehende Welle eine kugelförmige Welle ist, die Ausstrahlung auch eine kugelförmige Welle ist. Oder gemäß Marius' Gesetz ist der Lichtstreifen zwischen den entsprechenden Punkten vor und vor der eingehenden Welle ein fester Wert. Daher ist die Lichtstrecke zwischen dem Punkt A1 und seinem idealen Punkt Ak’ eine Konstante. Für ein optisches System mit k-Face, wie in Abbildung 4 gezeigt,

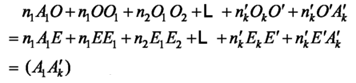
Der Raum des Objekts (einschließlich realer und virtueller Objekte) wird als Objektraum bezeichnet. Der Raum, in dem sich ein Bild befindet (sowohl physikalische als auch imaginäre Bilder), wird als Bildraum bezeichnet. Die beiden Räume erstrecken sich unendlich und sind nicht mechanisch durch die Brechungsoberfläche oder die linke und rechte Seite des optischen Systems getrennt.

Der Brechungsindex des Raummediums muss jedoch gemäß dem Brechungsindex des Raummediums vor dem System berechnet werden, in dem das tatsächliche eingehende Licht liegt. Der Brechungsindex eines räumlichen Mediums wie dieses muss auf der Grundlage des Brechungsindex des räumlichen Mediums hinter dem System berechnet werden, in dem das tatsächliche Licht abgegeben wird. Berechnen Sie, ob es sich um physische oder imaginäre Punkte, realistische oder imaginäre Punkte handelt.

Zum Beispiel wird der fiktive Punkt A in Abbildung 3 zwar positioniert hinter dem System, aber der Brechungsindex des Quadratraummediums wird immer noch gemäß dem Brechungsindex des Mediums im Raum berechnet, in dem das tatsächliche eingehende Licht (dh der Raum vor der Linse) auf den Punkt A gerichtet ist. . In ähnlicher Weise wird der Brechungsindex des Mediums im Raum berechnet, in dem das tatsächliche strahlende Licht (d. h. der Raum hinter der Linse) liegt, der dem imaginären Punkt A' entspricht.

Gemäß dem Theorem der Umkehrbarkeit des Lichtwegs, wenn der Punkt A' als Schnittpunkt betrachtet wird, muss das von A' emittierte Licht am Punkt A schneiden, und der Punkt A wird durch das optische System zu einem Bild, das von A' gebildet wird. Diese Korrespondenz zwischen dem Punkt A und dem Punkt A' wird als "Konjugation" bezeichnet.